데이터 개발 공부

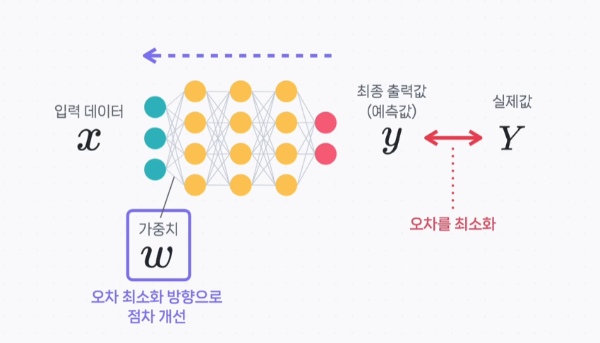
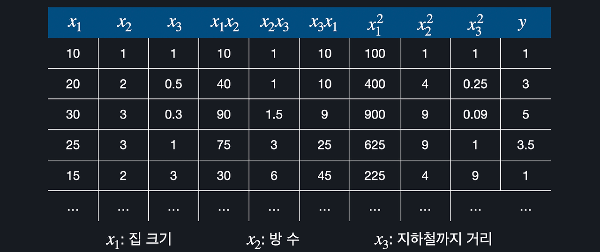
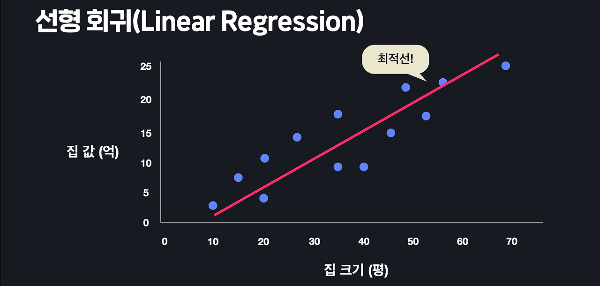
최적화가 어려운 이유1. 모델의 비선형성2. 고차원성과 과적합3. 그래디언트 소실 문제4. 하이퍼파라미터의 민감성하이퍼파라미터란?하이퍼파라미터란, 모델의 학습 과정에서 사용자가 사전에 설정해야 하는 값으로 모델의 성능 최적화를 위해 중요한 역할을 한다. 주로 딥러닝 학습 전에 설정되며, 학습 과정을 제어하는데 사용된다.모델의 학습 속도, 안정성, 최종 성능에 직접적인 영향을 미치며 적절한 하이퍼파라미터의 설정은 과적합 방지, 학습 효율, 모델 성능 최적화에 중요한 열할을 한다. 하이퍼파라미터의 종류1. 배치 크기(Batch Size)한 번의 학습 단계에 사용되는 데이터 샘플의 수이다. 이는 모델이 학습하는 데이터의 양을 결정해서 메모리 사용량과 학습 속도에 큰 영향을 미친다. 배치 크기가 작으면, 메모리..

로지스틱 회귀의 가설 함수와 손실 함수를 봤으므로 이제 경사 하강법을 알아보자.  가설 함수와 손실 함수는 좀 다르지만, 경사 하강법을 하는 방법은 선형 회귀와 거의 동일하다.  시작점을 위해 처음에는 세타 값들을 모두 0 또는 모두 랜덤으로 지정한다. 그러면 현재 세타 값들에 대한 손실, 즉 현재 가설 함수에 대한 손실을 계산할 수 있다. 여기서부터 시작해서 세타를 조금씩 조율하며 손실을 계속 줄여나가야 한다.  예를 들어, $θ_0, θ_1, θ_2$... 이렇게 세타 값이 3개 있다고 가정하자. 손실 함수를 $θ$에 대해 편미분하고, 그 결과에 학습률 알파를 곱한다. 그리고 그 결과를 기존 $θ_0$에서 빼면 된다. 똑같이 $θ_1$과 $θ_2$도 업데이트 하면 된다. 이렇게 모든 세타값들을 업데이..

선형 회귀를 통해 하려고 하는 건 학습 데이터에 최대한 잘 맞는 가설 함수를 찾는 것이다. 그러기 위해선 가설 함수를 평가하는 어떤 기준이 있어야 하는데, 그 기준이 되는게 손실 함수이다. 로지스틱 회귀에서도 마찬가지다. 데이터에 잘 맞는 가설 함수를 찾고, 손실 함수를 이용해 가설 함수를 평가한다. 선형 회귀의 손실 함수는 평균 제곱 오차라는 개념을 기반으로 하는데, 데이터 하나하나의 오차를 구한 후에 그 오차들을 모두 제곱항 평균을 내는 작업을 한다. 로지스틱 회귀의 손실 함수는 평균 제곱 오차를 사용하지 않고, 대신 '로그 손실', 영어로는 log loss라는 것을 사용한다. 좀 더 어려운 푷ㄴ으로는 cross entropy라고도 한다.  로그 손실로그 손실은 아래와 같은데, 이를 로그 손실이라고 ..

머신 러닝은 지도 학습과 비지도학습으로 나뉘는데, 지도 학습은 '회귀'와 '분류'로 나뉜다. 지도 학습회귀: 연속적인 값을 예측분류: 정해진 몇 개의 값 중에 예측ex. 어떤 이메일이 스팸인지 아닌지, 아니면 어떤 기사가 스포츠 기사인지 정치 기사인지 연예 기사인지 등 보통 분류 문제를 풀 때는, 각 결괏값에 어떤 숫자 값을 지정해 준다.예를 들어서 이메일이 스팸인지 아닌지 분류한다면, 보통 이메일에는 0이라는 값을 주고 스팸 이메일에는 1이라는 값을 주는 것이다. 이메일의 속성들을 가설 함수에 넣어서 0이 나오면 보통 이메일이고 1이 나오면 스팸 이메일이라고 할 수 있다.만약 어떤 기사가 스포츠 기사인지 정치 기사인지 연예 기사인지 분류하고 싶다면, 이번에는 가능한 결과가 3가지죠? 그러면 각각 0, ..

머신러닝 수업을 다 나갈 때 즈음미니 프로젝트, 그러니까 중간 프로젝트를 시작한다고 했다.  그렇게 시작된 약 3주간의 중간 프로젝트..! 팀은정말 고맙게도 먼저 제안해준 친구가 있어서 조심스레 합류했다.  '조심스레' 는..진짜 아직 초짜에 생초짜라 할 줄 아는게 있나 싶기도 하고...내 나이가 적지 않은터라 편하지만은 않을 텐데 이렇게 먼저 제안을 해줬다는게 고마우면서도 민폐가 되지 않을까노심초사했다.  우선 결과부터 말하자면잘했다.  중간 프로젝트라 조금 가벼운 마음으로 임했으나다른 친구들은 매우 진지하고 깊게 파고든 덕분에'대상'을 타게 되었다.수상은 토스뱅크 사무실 투어를 하는 날에 진행됐는데,그때 CTO님도 봤고멘토님들의 발표도 들을 수 있어서 좋았다.생각보다 더 동기부여가 뽱뽱 됐달까~귀여운..

딥 러닝 프레임워크딥 러닝 모델을 설계, 훈련, 검증하기 위해 사용되는 소프트웨어 라이브러리나 도구 모음 필요성- 복잡한 수치 계산과 미분을 자동화하여 효율성을 증대 시킬 수 있음- 모델 컴포넌트를 모듈화 하여 재사용 가능- 다양한 하드웨어 환경의 확장을 용이하게 함 주로 사용되는 프레임워크딥러닝의 기초 이론퍼셉트론(Perceptron)인공 신경망의 가장 기본적인 형태퍼셉트론을 구성하는 노드(Node)는 인공 신경망에서 정보를 처리하는 기본 단위라고 할 수 있다. 각 노드는 여러 입력값을 받아 이에 가중치를 곱한 후 합산하여 출력을 생성하는데, 신경망에서는 이러한 노드들이 서로 연결되어 있으며, 이 연결을 통해 데이터가 입력부터 출력까지 흐르게 된다.  초기 퍼셉트론의 구조는 이러한 노드 단위로 각 입력..

다항회귀란?선형 회귀는 학습 데이터에 가장 잘 맞는 일차식을 찾아서 예측을 하는 알고리즘인 반면, 다항 회귀는 고차식을 찾아서 예측하는 알고리즘이다.  집 값 예측 문제를 생각해보자. 항상 집의 크기라는 변수가 주어진다는 가정을 했고 이걸 하나의 속성으로 이용했는데 사용하는 데이터가 항상 이렇게 하나만 사용해도 의미가 있는 완벽한 변수일 수는 없다. 예를 들어 집이 사각형이라고 가정하고 집 크기 대신 집의 높이와 너비 데이터만 있다고 하자.사실 아무리 너비가 커도 높이가 작거나, 높이만 크고 너비만 작으면 크기가 작고 구조가 효율적이지 않기 때문에 집 값이 높지 않다. 사실 이 두 변수들보다 집값을 예측하는 데 훨씬 좋은 수치는 이 둘을 곱한 값, 집의 넓이다.단순 선형 회귀를 사용하면 이 두 변수가 서..

다중 선형회귀는 선형 회귀를 하나의 입력 변수가 아닌 여러개의 입력 변수를 사용하여 목표 변수를 예측하는 알고리즘이다.  예를 들어, 아래와 같은 학습 데이터가 있으면,집크기, 방 수, 연식, 지하철까지의 거리 등등 을 이용하여 선형 회귀를 통해 집 값을 혜측하려는 것이다. 다중 선형 회귀 문제 표현위의 집 값 예측에 따른 표를 보면 입력 변수는 '집 크기(평), 방 수, 건물 나이(년), 지하철 거리(m)'로 4개의 변수가 있다. 입력 변수를 다른 말로는 '속성(feature)'라고 한다. 첫 번째 입력 변수는 $x_{1}$, 두 번째 입력 변수는 $x_{2}$ 처럼 밑첨자로 변수의 종류를 구분하여 나타낸다.여기서 입력 변수의 개수는 n으로 표현하는데, 위의 표에 따르면 입력 변수가 총 4개이기 때문에..

선형 회귀 (Linear Regression)우선 집 크기가 주어졌을 때, 집 값을 예측한다고 해보자. 이때 선형 회귀는 여기 있는 데이터를 가장 잘 대변해 주는 선을 찾아내는 것이다. 이 데이터에 가장 잘 맞는, 가장 적절한 하나의 선을 찾아내는 거다. 통계학에서는 최적선, 영어로는 line of best fit이라고도 한다. 위의 이미지와 같이 데이터에 잘 맞는 최적선을 찾았다고 가정해보자. 그럼 이걸 어떻게 활용할 수 있을까? 아래 이미지의 최적선을 보면 50평 집 가격은 20억으로, 30평인 집은 약 10억 5천만원이라고 볼 수 있다. 이처럼 정확하진 않더라도 꽤나 합리적인 예측을 할 수 있다. 변수위의 예에서 우리가 맞추려고 하는 '집 가격'은 '목표 변수(target variable)' 또는 ..

정규화(Regularization)란?복잡한 모델을 그대로 학습시키면 과적합이 된다. 이때, '정규화' 라는 기법을 통해 학습 과정에서 모델이 과적합 되는 것을 예방할 수 있다. 아래 좌측 이미지와 같은 학습 데이터를 이용하여 다항 회귀를 해보면 우측 이미지처럼 모델이 과적합되어 복잡한 다항 함수가 나오게 된다.  과적합된 함수는 보통 위아래로 엄청 왔다 갔다 하는 특징이 있다. 많은 굴곡을 이용하여 함수가  training데이터를 최대한 많이 통과하도록 하는 것이다. 함수가 이렇게 급격히 변화한다는 것은 함수의 계수, 즉 가설 함수의 θ값들이 굉장히 크다는 의미이다.  정규화는 모델을 학습시킬 때 θ 값들이 너무 커지는 것을 방지해준다. θ 값들이 너무 커지는 걸 방지하면 아래 이미지처럼 trainin..