다중 선형회귀는 선형 회귀를 하나의 입력 변수가 아닌 여러개의 입력 변수를 사용하여 목표 변수를 예측하는 알고리즘이다.
예를 들어, 아래와 같은 학습 데이터가 있으면,
집크기, 방 수, 연식, 지하철까지의 거리 등등 을 이용하여 선형 회귀를 통해 집 값을 혜측하려는 것이다.

다중 선형 회귀 문제 표현
위의 집 값 예측에 따른 표를 보면 입력 변수는 '집 크기(평), 방 수, 건물 나이(년), 지하철 거리(m)'로 4개의 변수가 있다.
입력 변수를 다른 말로는 '속성(feature)'라고 한다.
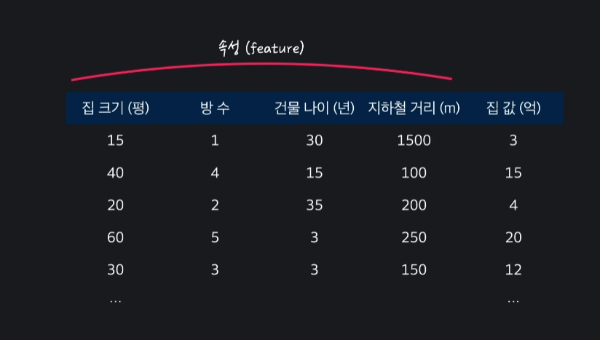
첫 번째 입력 변수는 $x_{1}$, 두 번째 입력 변수는 $x_{2}$ 처럼 밑첨자로 변수의 종류를 구분하여 나타낸다.

여기서 입력 변수의 개수는 n으로 표현하는데, 위의 표에 따르면 입력 변수가 총 4개이기 때문에 n=4가 된다.
그리고 목표 변수는 1개이며 y로 나타낸다.
또, 학습 데이터의 개수는 m이라는 문자로 표현하는데, 집 가격을 예측하는 프로그램을 만들 때 m이 50이면 50개의 집 데이터를 가지고 프로그램을 학습시키게 된다.

1번째 집의 입력 변수는 $x^{(1)}$로 x의 위첨자에 (1)을 써서 표현한다. 그럼 1번째 집의 목표 변수는 $y^{(1)}$으로 표현된다.
마찬가지로 $x^{(1)}$은 3번째 입력 변수이고 목표 변수는 $y^{(1)}$ 으로 표현되게 된다.



그렇다면 3번째 데이터의 2번째 속성인 방 수를 나타내고 딮다면 어떻게 해야 할까?

$x^{(1)}_2$ 로 표현되며, 일반화하자면 i번째 데이터의 j번째 속성은 $x^{(i)}_j$ 로 나타낼 수 있다.

다중 선형 회귀 가설 함수

- : 입력 x에 대한 예측값(출력)
- $\theta_0$: 절편(intercept), 상수항
- $\theta_1$: 기울기(slope)
- x: 입력 변수





다중 선형 회귀에서도 가설 함수의 목적은 근본적으로 좋은 가설 함수를 만들고 최대한 정확하게 예측하기 위해 세타 값들을 조금씩 조율하면서 학습 데이터에 가장 잘 맞는 세타 값들을 찾아내는 것이다.
이때, 위의 복잡하고 긴 함수를 선형대수학의 벡터를 이용해 간결하게 표현할 수 있다.
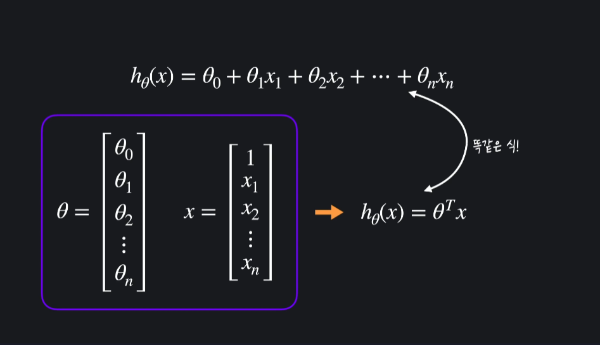
즉, 가설 함수는 이렇게 표현된다.
$h_\theta (x) = \theta ^Tx$

예제 - prediction 함수
다중 선형 회귀의 가정 함수를 prediction 함수로 구현해보자.
아래와 같다고 할 때, 라고 할 때, 모든 학습 데이터에 대한 예측 값들을 그냥 간단하게 Xθ로 나타낼 수 있다. 이 부분을 구현해보자.
가정 함수 prediction은 파라미터로 입력 변수 X를 나타내는 X 그리고, 파라미터 θ를 나타내는 theta를 받습니다. 이 두 파라미터를 갖고 모든 데이터의 예측 값을 numpy 배열로 리턴하는 함수 prediction을 구현해보세요!

import numpy as np
def prediction(X, theta):
"""다중 선형 회귀 가정 함수. 모든 데이터에 대한 예측 값을 numpy 배열로 리턴한다"""
return X @ theta
# 입력 변수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0]) # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0]) # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4]) # 방 수
# 설계 행렬 X 정의
X = np.array([
np.ones(16),
house_size,
distance_from_station,
number_of_rooms
]).T
# 파라미터 theta 값 정의
theta = np.array([1, 2, 3, 4])
prediction(X, theta)
# 출력값
array([ 22. , 21.8, 21.2, 26.7, 24.7, 24.8, 25.5, 26.2, 29.7,
31.4, 33.1, 33.9, 39. , 39.4, 39.5, 40. ])다중 선형 회귀 경사 하강법
데이터에 최대한 잘 맞는 최적선을 찾기 위해 시도해보는 선 하나하나를 가설 함수라고 한다.
그런데 가설 함수가 얼마나 좋은지, 어떻게 개선해야 할 지 알기 위해선 가설 함수를 평가하는 기준이 필요한데 이를 손실 함수로 평가하게 된다.

위의 수식을 보면 손실 함수는 세타에 대한 함수인 것을 알 수 있다. 가설 함수가 어떤 세타 값을 쓰냐에 따라 이 손실 함수의 결과가 달라진다. 손실 함수의 결괏값이 크다는 것은 손실이 크다는 것이므로 좋지 않은 가설 함수고, 반대로 손실 함수의 결괏값이 작으면 손실이 작은 것이므로 좋은 가설 함수라고 할 수 있다.

선형 회귀에서는 세타 값들을 잘 선택하여 이 손실 함수의 결괏값을 최대한 작게 만드는 것이었다. 이를 하기 위한 방법 중 하나로 '경사 하강법'을 사용했는데 '경사 하강법'은 손실 함수의 아웃풋을 낮추기 위해 가장 가파르게 내려가는 방향으로 계속해서 이동하는 것이다.
즉, 손실을 가장 빠르게 줄일 수 있는 방향으로 세타 값들을 수정하는 것이다.
그럼 다중 선형 회귀에서는 어떻게 할까?
시각적으로 표현하는 건 어렵지만 수학적으로(?)는 거의 동일하다고 볼 수 있다.
다중 선형 회귀에서도 손실 함수는 똑같이 생겼다.

다중 선형 회귀에서는 입력 변수가 여러 개라서 가설 함수가 살짝 달라지지만, 손실 함수는 완전히 동일하다.
또, 손실을 줄이기 위해선 경사 하강법을 해야 하는데 입력 변수가 하나일 때는 $\theta_0$과 $\theta_1$만 업데이트 하면 되었다.

그렇다면 입력 변수가 여러개일 때에는 세타 값도 여러개가 되는데 업데이트할 세타 값이 많아지게 되는 것 뿐이다.

위 이미지와 같이 입력 변수가 n개 있다고 하면 $\theta_0$
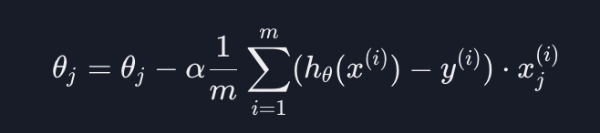
j에 0부터 n까지 넣어서 모든 세타 값들을 업데이트하는 것이다.

이러한 과정을 한 번 거칠 때마다, 손실을 최대한 빨리 감소시키는 방향으로 세타 값들이 업데이트 된다.
이 작업을 충분히 반복하면 결국 손실을 최소에 가깝게 줄일 수 있다. 그러면 학습 데이터에 잘 맞는 세타 값들을 찾게 되는데, 데이터에 잘 맞는 가설 함수를 찾았다고 할 수 있게 된다.
예제 - gradient_descent 함수

import numpy as np
def prediction(X, theta):
"""다중 선형 회귀 가정 함수. 모든 데이터에 대한 예측 값을 numpy 배열로 리턴한다"""
return X @ theta # X와 theta의 행렬 곱을 사용하여 예측 값 반환
def gradient_descent(X, theta, y, iterations, alpha):
"""다중 선형 회귀 경사 하강법을 구현한 함수"""
m = len(X) # 입력 변수 개수 저장
for _ in range(iterations):
# 코드를 쓰세요
error = prediction(X, theta) - y
theta = theta - alpha / m * (X.T @ error)
return theta
# 입력 변수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0]) # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0]) # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4]) # 방 수
# 목표 변수
house_price = np.array([3, 3.2, 3.6 , 8, 3.4, 4.5, 5, 5.8, 6, 6.5, 9, 9, 10, 12, 13, 15]) # 집 가격
# 설계 행렬 X 정의
X = np.array([
np.ones(16),
house_size,
distance_from_station,
number_of_rooms
]).T
# 입력 변수 y 정의
y = house_price
# 파라미터 theta 초기화
theta = np.array([0, 0, 0, 0])
# 학습률 0.01로 100번 경사 하강
theta = gradient_descent(X, theta, y, 100, 0.01)
theta
# 출력값
array([ 0.11484521, 1.21120425, 0.18270523, 0.30060782])정규방정식


예제 - normal_equation 함수

import numpy as np
def normal_equation(X, y):
"""설계 행렬 X와 목표 변수 벡터 y를 받아 정규 방정식으로 최적의 theta를 구하는 함수"""
theta = np.linalg.pinv(X.T @ X) @ X.T @ y
return theta
# 입력 변수
house_size = np.array([1.0, 1.5, 1.8, 5, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.0, 7.0, 8.0, 8.5, 9.0, 10.0]) # 집 크기
distance_from_station = np.array([5, 4.6, 4.2, 3.9, 3.9, 3.6, 3.5, 3.4, 2.9, 2.8, 2.7, 2.3, 2.0, 1.8, 1.5, 1.0]) # 지하철역으로부터의 거리 (km)
number_of_rooms = np.array([1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4]) # 방 수
# 목표 변수
house_price = np.array([3, 3.2, 3.6 , 8, 3.4, 4.5, 5, 5.8, 6, 6.5, 9, 9, 10, 12, 13, 15]) # 집 가격
# 입력 변수 파라미터 X 정의
X = np.array([
np.ones(16),
house_size,
distance_from_station,
number_of_rooms
]).T
# 입력 변수 y 정의
y = house_price
# 정규 방적식으로 theta 계산
theta = normal_equation(X, y)
theta
# 출력값
array([ 5.24706322, 1.30727421, -0.68881811, -0.8709494 ])선형 회귀의 손실 함수 J(θ) 를 최소화하는 θ를 찾는 두 가지 방법 비교

위의 표와 같은 차이가 있다면 둘 중 어떤 걸 선택해야 될까?
절대적으로 정해진 것은 없다. 다만,
- 입력 변수(속성)의 수가 엄청 많을 때는(1000개를 넘느냐를 기준으로 사용할 때가 많음) -> 경사 하강법
- 비교적 입력 변수의 수가 적을 때 -> 정규 방정식
을 사용한다.
Convex 함수
손실 함수 J(θ)의 경사를 구한 뒤에 이걸 이용해서 최솟값을 갖는 θ를 찾았다.
근데 단순히 경사 하강법과 정규 방정식만 이용하면 항상 손실 함수의 최소 지점을 찾을 수 있을까?
아래와 같은 함수에서 경사 하강법을 한다고 해보자.

이 지점에서 시작을 해서 경사를 따라 쭉 내려간다. 내려가다가 보면 어느 순간 여러 극소값 중 하나에 오고 여기서는 경사가 0이어서 경사 하강이 종료가 된다. 그럼 손실 함수의 최저점을 찾아갈 수가 없습니다.
정규 방정식도 마찬가지다.

이렇게 수많은 극소값들과 극대값들이 있으면 아무리 방정식을 해결해도 구한 수많은 지점 중에서 어떤 지점이 최소점인지를 알 수가 없다.
이 모든 지점들이 경사가 0일테니까.
그러니까 함수가 이런 식으로 생긴 경우에는 경사 하강법과 정규 방정식을 통해서 구한 극소 지점이 손실 함수 전체에서 최소 지점이라고 확실하게 얘기할 수가 없다.
반대로 손실 함수가 이렇게 생겼다고 해보자.
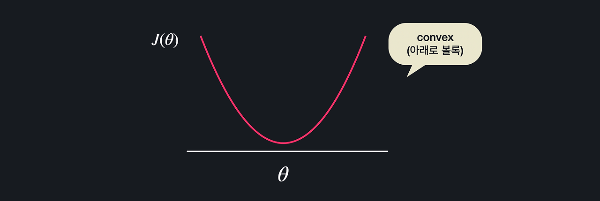
이 함수는 어떤 지점에서 경사 하강을 시작해도 항상 손실 함수의 최소 지점을 찾을 수 있고, 정규 방정식을 이용해서 최소점을 구할 수 있다.
이런 함수를 convex 함수(아래로 볼록한 함수)라고 부른다.
convex 함수에서는 항상 경사 하강법이나 정규 방정식을 이용해서 최소점을 구할 수 있는 반면, 노트 위에서 봤던 non-convex 함수에서는 구한 극소점이 최소점이라고 확신할 수 없다.
선형 회귀의 평균 제곱 오차
선형 회귀에서는 가정 함수의 예측값들과 실제 목표 변수들의 평균 제곱 오차(MSE)를 손실 함수로 사용했다. 다행히 선형 회귀 손실 함수로 사용하는 MSE는 항상 convex 함수다. 그러니까 선형 회귀를 할 때는 경사 하강법을 하거나 정규 방정식을 하거나 항상 최적의 θ 값들을 구할 수 있는 것이다.
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import pandas as pd
boston_dataset = load_boston()
X = pd.DataFrame(boston_dataset.data, columns=boston_dataset.feature_names)
y = pd.DataFrame(boston_dataset.target, columns=['MEDV'])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=5)
model = LinearRegression()
model.fit(X_train, y_train)
model.coef_ # 세타값(회귀계수)
model.intercept_ # 세타0값(절편)
y_test_prediction = model.predict(X_test)
mean_squared_error(y_test, y_test_prediction) ** 0.5
# 출력값
# 4.5682920423031774
# 위 모델로 예측 시, 약 4천 5백달러 정도의 오차가 발생
# -> 이전 선형회귀에서 입력변수 하나만 가지고 진행했을 땐, 8200달러 정도 나옴
# -> 입력 변수를 많이 사용하여 다중 선형 회귀를 진행하니 오차가 크게 줄어든 걸 알 수 있음예제 - 당뇨 추치 예측하기

# 필요한 라이브러리 import
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import pandas as pd
# 당뇨병 데이터 갖고 오기
diabetes_dataset = datasets.load_diabetes()
# 입력 변수를 사용하기 편하게 pandas dataframe으로 변환
X = pd.DataFrame(diabetes_dataset.data, columns=diabetes_dataset.feature_names)
# 목표 변수를 사용하기 편하게 pandas dataframe으로 변환
y = pd.DataFrame(diabetes_dataset.target, columns=['diabetes'])
# train_test_split를 사용해서 주어진 데이터를 학습, 테스트 데이터로 나눈다
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=5)
linear_regression_model = LinearRegression() # 선형 회귀 모델을 가지고 오고
linear_regression_model.fit(X_train, y_train) # 학습 데이터를 이용해서 모델을 학습 시킨다
y_test_predict = linear_regression_model.predict(X_test) # 학습시킨 모델로 예측
# 평균 제곱 오차의 루트를 통해서 테스트 데이터에서의 모델 성능 판단
mse = mean_squared_error(y_test, y_test_predict)
mse ** 0.5
# 출력 결과
# 54.603896119844421