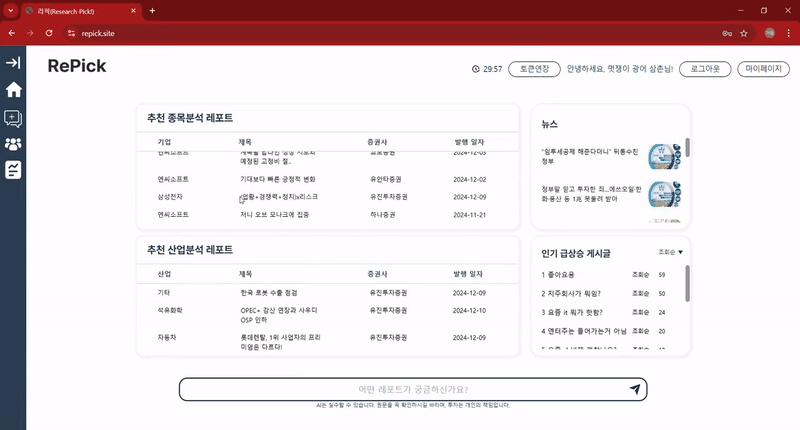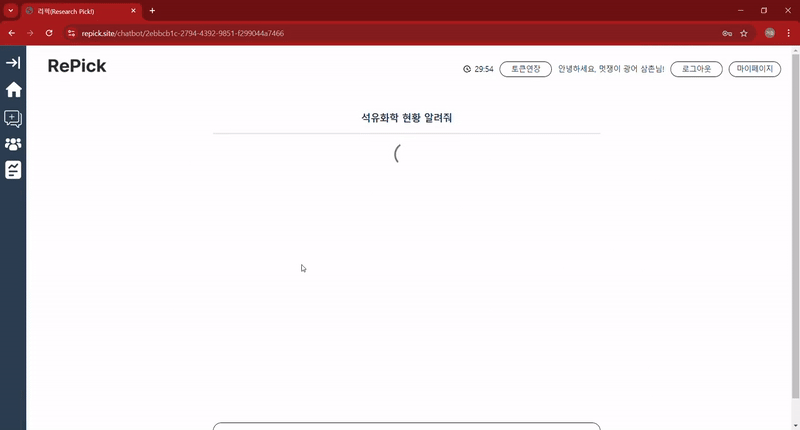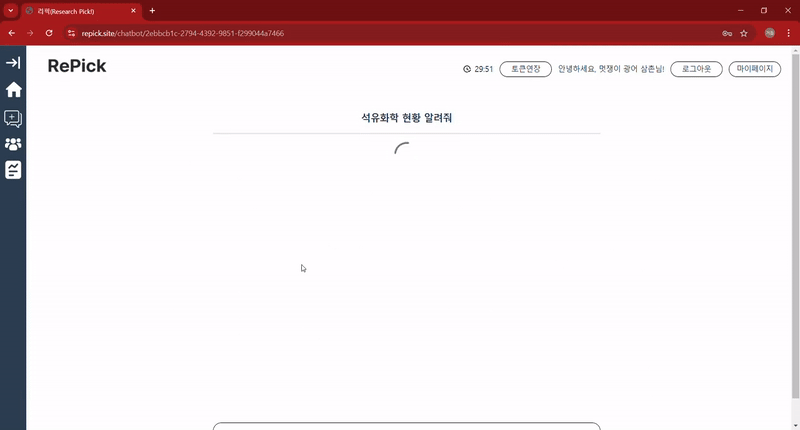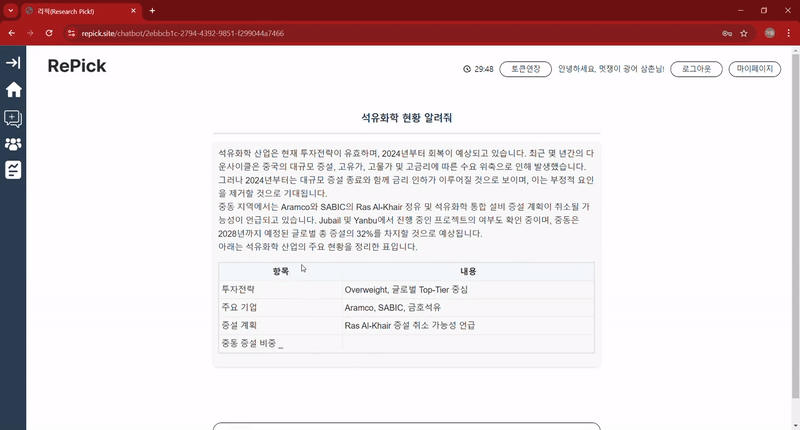
👇 이전 포스팅은 아래에서 확인할 수 있습니다. 👇 1️⃣ 금융 데이터 AI 챗봇 개발기: 1) 그래서 PDF를 어떻게 분석할건데? (기획부터 데이터 전처리까지) - 출처: https://nanini.tistory.com/902️⃣ 데이터 AI 챗봇 개발기: 2) LLM 모델을 통한 챗봇 만들기 (RAG부터 Chain까지) - 출처: https://nanini.tistory.com/913️⃣ 금융 데이터 AI 챗봇 개발기: 3) 추천 알고리즘, 개인 선호도를 반영한 레포트 추천 기능 만들기- 출처: https://nanini.tistory.com/92 앞에서 세 개 포스팅으로 모델을 구현한 이야기의 최종판, 기능들을 한데 모아서RePick이란 서비스를 만들었다. - RePick (ht..