딥 러닝 프레임워크
딥 러닝 모델을 설계, 훈련, 검증하기 위해 사용되는 소프트웨어 라이브러리나 도구 모음
필요성
- 복잡한 수치 계산과 미분을 자동화하여 효율성을 증대 시킬 수 있음
- 모델 컴포넌트를 모듈화 하여 재사용 가능
- 다양한 하드웨어 환경의 확장을 용이하게 함
주로 사용되는 프레임워크


딥러닝의 기초 이론
퍼셉트론(Perceptron)
인공 신경망의 가장 기본적인 형태

퍼셉트론을 구성하는 노드(Node)는 인공 신경망에서 정보를 처리하는 기본 단위라고 할 수 있다. 각 노드는 여러 입력값을 받아 이에 가중치를 곱한 후 합산하여 출력을 생성하는데, 신경망에서는 이러한 노드들이 서로 연결되어 있으며, 이 연결을 통해 데이터가 입력부터 출력까지 흐르게 된다.
초기 퍼셉트론의 구조는 이러한 노드 단위로 각 입력값에 가중치를 곱하고, 이들의 합이 특정 임계치를 넘으면 출력값으로 1을, 넘지 않으면 0을 출력하는 형태로 0 또는 1의 출력을 생성했다.
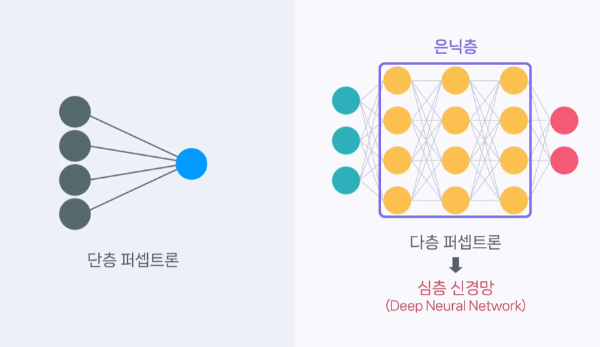
하지만 입력층과 출력층으로 구성된 단층 퍼셉트론은 간단한 패턴의 데이터 처리에는 유효하지만, 복잡한 데이터 패턴을 학습하기에는 무리가 있었다.

이후 입력층과 출력층 사이에 은닉층을 포함한 다층 퍼셉트론(MLP)이 등장했다.
다층 퍼셉트론(Multi-Layer Perceptron)

레이어는 여러 노드들이 모인 집합으로, 신경망의 구조를 구성하는 단위다.

신경망은 일반적으로 입력층, 은닉층, 출력층으로 구성되는데,
은닉층이 없는 경우를 '단층 퍼셉트론', 하나 이상 포함된 경우를 '다층 퍼셉트론'이라고 한다.
은닉층
은닉층은 필요에 따라 여러 개를 추가할 수 있으며, 이러한 은닉층을 여러개 가진 깊은 신경망을 '심층 신경망(DNN)'이라고 한다.
다층 퍼셉트론을 사용하면 좀 더 복잡한 결졍 경계를 형성할 수 있다.
은닉층은 입력층과 출력층 사이에 위치하며,
네트워크의 입력과 출력 사이에서 복잡한 특성이나 패턴을 추출하고 학습하는 역할을 한다.
은닉층을 통해 네트워크는 비선형적인 데이터의 특성을 학습하고, 보다 정교한 모델을 구축할 수 있다.

다층 퍼셉트론에서는 입력 데이터에 가중치를 곱하고, 이 결과를 합하여 여러 은닉층을 통해 전파하는 순전파 과정을 거친다. 그리고 이때 시그모이드 같은 비선형 활성화 함수를 사용한다.
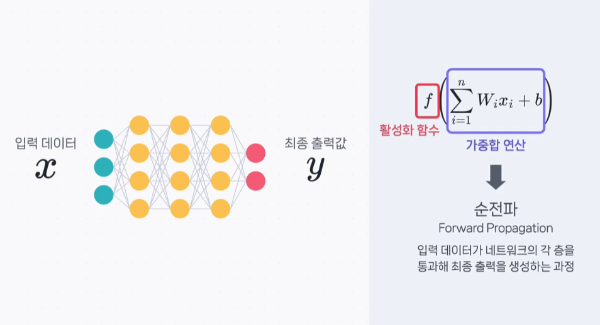
순전파
순전파란, 신경망에서 입력 데이터가 네트워크의 각 층을 순차적으로 통과하여 최종 출력을 생성하는 과정을 말하는데
이 과정에서 각 층의 뉴런은 활성화 함수를 사용하여 다음 층으로의 출력을 생성한다.

결과적으로 생성된 출력된 값은 '예측값'으로 사용되며,
이 예측값을 실제값과 비교하는 손실함수를 통해 네트워크의 성능을 평가하고 최적화한다.
손실 함수는 모델의 예측이 실제 데이터와 얼마나 차이가 나는지를 측정하고, 이 정보를 바탕으로 모델의 학습을 조정한다.
또, 다층 퍼셉트론에서는 은닉층을 여러개 쌓을 뿐 아니라 Sigmoid 같은 비선형 활성화 함수를 사용한다는 특징이 있는데
은닉층을 여러개 쌓아도 활성화 함수가 선형이면 비선형 연산은 불가능하다고 볼 수 있다.
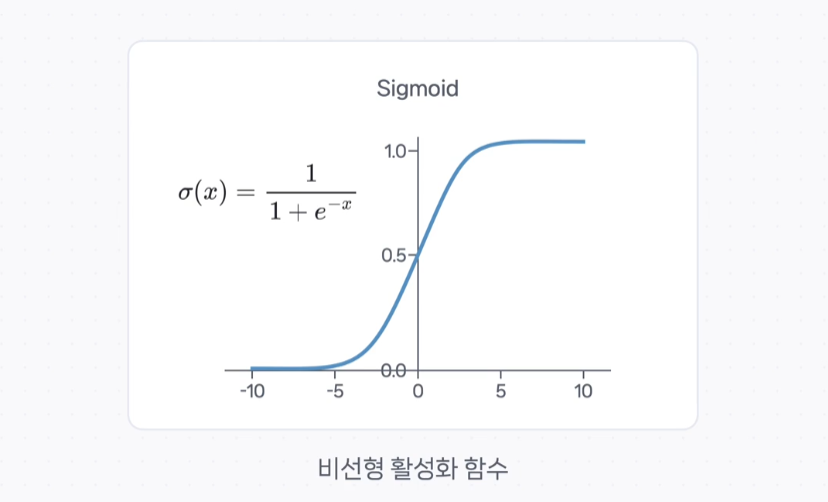
그래서 각 층마다 비선형 활성화 함수를 적용해서 좀 더 복잡한 데이터 패턴을 효과적으로 학습할 수 있도록 한다.
이 외에도 다양한 활성화 함수가 있는데, 각기 다른 특성을 통해 신경망의 성능을 개선하는데 기여한다.

출력 함수
딥러닝에서 매우 중요한 역할을 한다.
출력 함수는 신경망의 마지막 층에 위치하여 신경망을 통해 계산된 값을 최종 결과 형태로 변환해 준다.
예를 들어, 회귀나 분류 문제를 해결할 때 출력 함수가 필수적으로 사용된다.

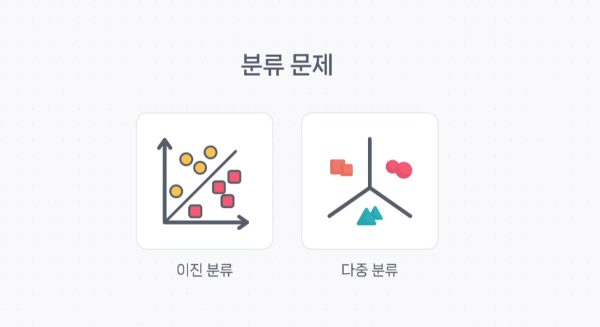
이진 분류 문제
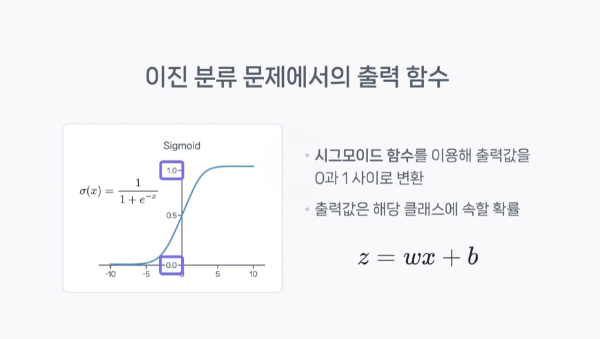
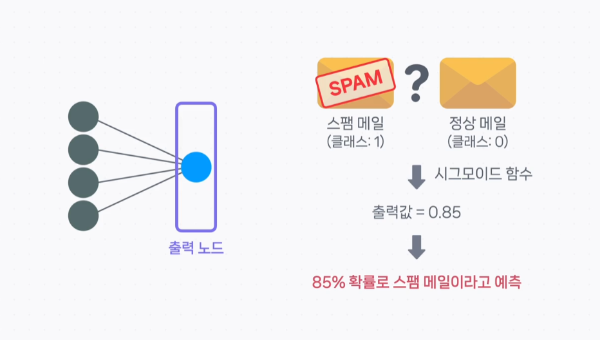
보통 확률이 0.5 이상일 경우, 해당 클래스가 맞다고 분류한다.
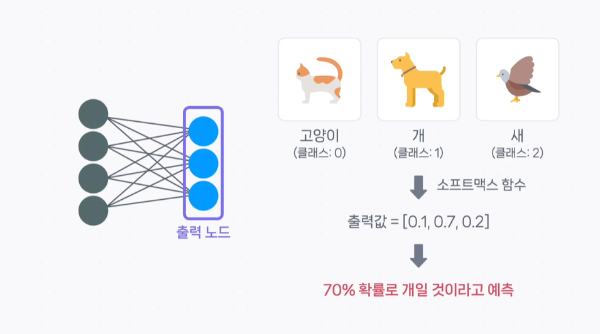
다중 분류 문제

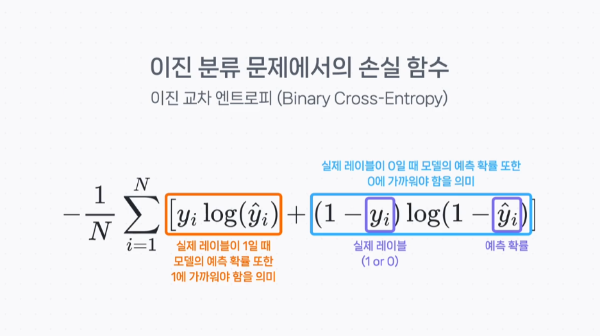
손실 함수

회귀 문제


분류 문제



소프트맥스 활성화 함수는 다중 클래스 분류 문제에서 사용되며, 각 클래스에 대한 출력값을 확률 분포로 변환하여 제공한다. 이는 출력층에서 각 클래스에 속할 확률을 추정하는 데 효과적이다.
역전파(Backpropagation)
딥러닝 모델이 잘 학습되었다는 것은
예측 결괏값이 실제 값에 가까워지며 오차가 최소화된 상태를 의미한다고 볼 수 있는데, 이때 오차를 줄이고, 가중치를 최적의 값으로 잘 업데이트 하기 위해서는 역전파라는 것이 중요한 역할을 한다.
역전파는 출력에서 발생한 오차를 신경망을 거슬러 올라가며 각 층의 가중치에 대한 오차의 기여도를 계산하고,
이 정보를 사용하여 가중치를 업데이트 한다.

역전파는 출력에서 발생한 오차를 신경망을 거슬러 올라가며 각 층의 가중치에 대한 오차의 기여도를 계산하고, 이 정보를 사용하여 가중치를 업데이트한다.
이를 통해 오차를 최소화하는 것을 목표로 학습이 이루어지게 된다.

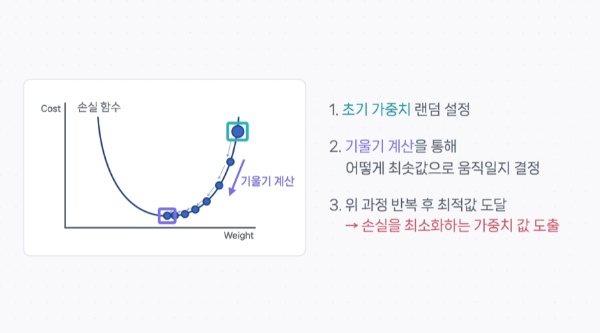
경사하강법


신경망의 역전파를 이해하기 위해 필요한 두 가지 중요한 미적분학 관련 개념이 있다.
바로 편미분과 합성 함수의 미분이다.
편미분
다변수 함수에서 한 변수의 변화가 함수에 미치는 영향을 측정하기 위해 사용된다.
다른 모든 변수는 상수로 간주하면서 해당 변수에 대해서만 미분을 진행하는 것이다.
예를 들어,
함수 $f(x,y) = x^2y+3xy+y^2$에서 $x$에 대한 편미분을 계산하면, $y$를 상수로 간주하고 $x$에 대해서만 미분을 수행한다.

합성 함수의 미분
복잡한 함수들이 서로 결합되어 있을 때 사용된다.
이는 체인룰(Chain Rule)이라고 하는 규칙을 사용하여 외부 함수의 미분과 내부 함수의 미분을 곱해 전체 미분을 구하는 방식이다.
예를 들어,
$y=f(g(x))$의 형태를 갖는 함수에서 $x$에 대한 $y$의 미분을 구하면, $g(x)$의 미분과 $f(g)$의 미분을 곱하여 아래와 같이 계산한다.
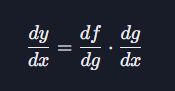
신경망은 이렇게 복잡한 합성 함수로 구성되어 있다. 신경망에서 각 레이어는 가중합 연산과 활성화 함수를 포함하고 있으며, 이 두 요소가 결합되어 하나의 함수를 형성한다. 이렇게 각 레이어를 거치면서 다양한 함수들이 결합되어, 전체 신경망은 연속적인 합성 함수로 구성된다고 볼 수 있다.
이러한 구조 때문에 신경망을 미분할 때는 합성 합수의 미분법을 적용한다.
역전파, 순전파 과정에서의 계산 과정
순전파(Forward Propagation)
입력 데이터가 네트워크의 처음부터 끝까지 흘러가는 과정을 말한다.
이 과정에서 각 레이어는 입력 데이터에 대해 선형 변환(ex. 가중치와 편향을 이용한 계산)과 활성화 함수(ex. ReLU, Sigmoid)를 적용한다.
이러한 계산을 통해 입력 데이터는 최종적으로 출력층에 도달하고, 모델은 예측 결과를 생성한다.
계산 과정을 알아보기 위해 간단한 예시를 살펴보자.
입력 데이터는 $x$, 각 층에서 적용할 가중치 값은 $w1$와 $w2$이다. 일단 입력 $x$에 가중치 $w1$을 곱한 후 시그모이드 함수를 적용하여 출력값 a1을 생성한다.
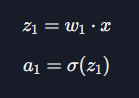
이 출력값 a1은 다음 층으로 전달된다.
이게 출력층이라고 하면, a1에 가중치 $w2$을 곱하여 최종적으로 예측값 $y_pred$ 를 계산하게 되는데, 이 과정을 통해 입력 데이터는 초기 단계에서 처리되어 최종적인 예측 결과를 생성하게 된다.

역전파(Backpropagation)
모델의 예측 결과와 실제 값과의 차이(손실)을 계산한 후, 이 손실 값을 사용하여 모델의 각 파라미터(가중치)를 조정하는 과정이다. 손실 함수를 통해 계산된 손실을 기반으로, 앞서 배운 Chain Rule 을 이용해 각 레이어와 뉴런의 가중치에 대한 손실의 미분값(기울기)를 계산하고, 이 기울기를 사용하여 가중치를 업데이트 한다.
우리가 현재 고려하고 있는 단층 퍼셉트론에서는 순전파 과정을 통해 입력 데이터를 받아 최종 예측값 $y_pred$ 를 생성하고, 이 값을 사용하여 신경망의 성능을 평가하는데, 이때 손실 함수로는 아래와 같은 평균 제곱 오차(Mean Squared Error, MSE)를 사용해보자.

신경망의 주된 목표는 이 손실 함수의 값을 최소화 하는 것이며, 이를 위해 역전파 과정을 통해 가중치 $w1$과 $w2$를 업데이트 한다.
역전파 과정은 순전파의 반대 방향으로 진행되며, 이 과정에서 가중치에 대한 손실 함수의 그래디언트(미분값)을 계산하는데, Chain Rule을 사용하여 이 그래디언트를 계산하고, 계산된 그래디언트는 가중치의 업데이트를 위해 사용된다.
구체적으로, 손실 함수 $L$에 대해 $w2$의 그래디언트를 먼저 계산하고, 이어서 $w1$의 그래디언트를 계산한다. 이러한 그래디언트 계산은 각 가중치의 영향을 평가하고, 가중치를 조정함으로써 손실을 줄이는 방향으로 신경망을 조정하는 데 중요한 역할을 한다.
이렇게 역전파를 통한 가중치 업데이트는 신경망이 학습하고 성능을 개선하도록 돕는다.
먼저,
위 손실함수를 $y_pred$에 대해 미분한 $∂L/∂y_pred$값은 아래와 같다. 이 값을 Chain Rule 적용과정에서 사용해보자.
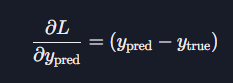
역전파 과정에서, 출력층의 가중치 $w2$에 대한 손실 함수의 그래디언트는 Chain Rule을 사용하여 계산된다.
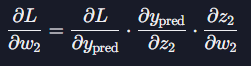
가중치 $w1$에 대한 그래디언트도 비슷한 방식으로 계산된다.
이 그래디언트는 다음과 같은 세 개의 미분값을 연쇄적으로 곱해서 구할 수 있는데, 각각 $∂z2/∂a1$은 $w2$, $∂z1/∂w1$은 입력 $x$, $∂a1/∂z1$은 $σ′(z1)$와 같다. 이 모든 미분값들을 연쇄적으로 곱하는 것으로 $w1$에 대한 그래디언트를 계산하며, 이는 모델의 가중치를 업데이트하는 데 사용된다.

이제 본격적으로 경사 하강법을 통해 $w1$와 $w2$를 업데이트해 보자.
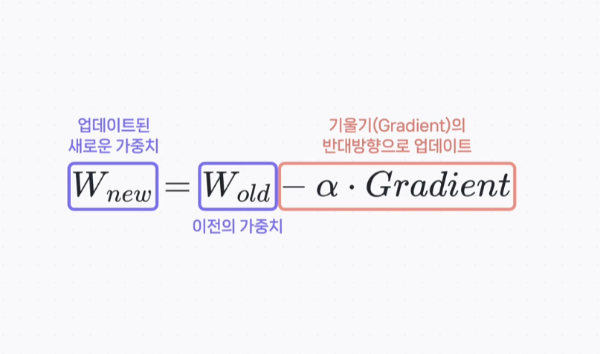
경사 하강법은 머신 러닝과 딥 러닝에서 널리 사용되는 최적화 기법으로, 모델의 손실 함수를 최소화하기 위해 가중치를 반복적으로 조정하는 방법인데, 이 과정에서 계산된 각 가중치에 대한 손실 함수의 그래디언트를 사용하여 가중치를 업데이트한다. 구체적으로, 각 가중치 w의 업데이트는 다음과 같은 식으로 표현할 수 있다.

위 공식을 이용해 위에서 계산한 각 가중치의 그래디언트에 대해서 업데이트 하는 과정은 아래와 같다. 참고로$w1$도 동일하게 적용된다고 볼 수 있다.
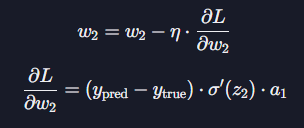
위 과정을 통해 각 가중치 $w1$과 $w2$는 주어진 데이터에 대해 손실을 최소화하는 방향으로 조정된다.