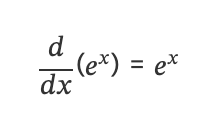예측 모형의 성능
손실함수(loss function)
= 비용함수(cost function) 또는 오차함수(error function)
목적: 목적함수의 값을 가장 크게 혹은 적게 할 수 있는 입력값, 즉 모수를 구하는 것을 최적화(optmization)라고 한다.
eg.
미분을 이용해 최소 지점으로 갈 수 있는 방법을 구해보자.
기울기
: (= 변화량) 가장 적은 횟수로 여러가지 𝑥값을 시도하여 최적의 값을 찾는 방법

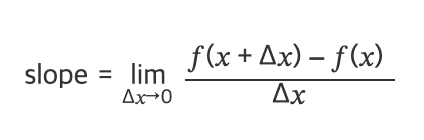
수치미분

미분(differentiation)
: 어떤 함수로부터 그 함수 기울기를 출력하는 새로운 함수를 만들어내는 작업이다. 미분으로 만들어진 함수를 원래 함수의 도함수(derivative)라고 한다.
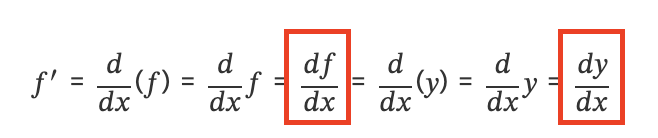
미분 가능
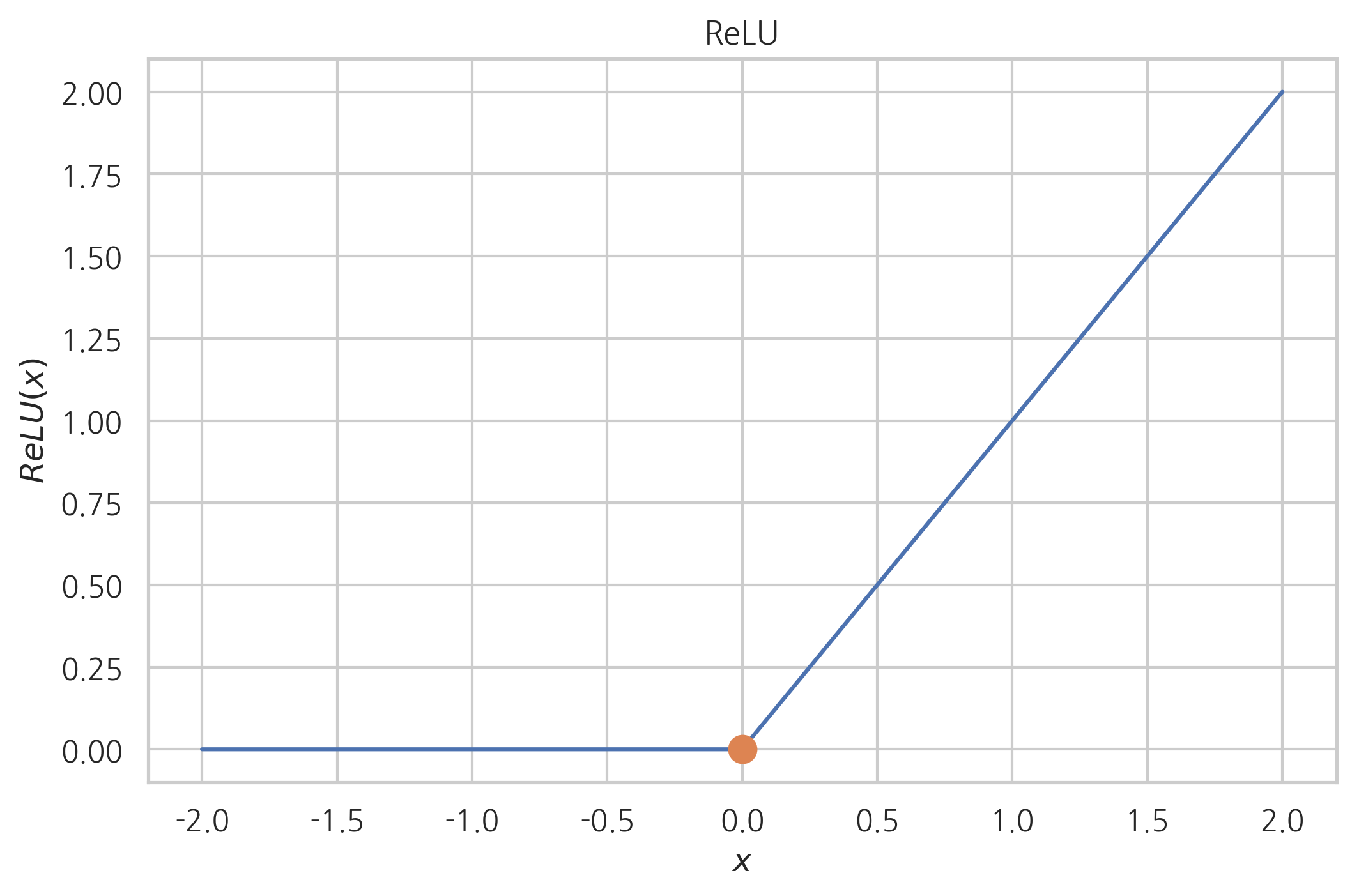
: 함수에 따라서는 어떤 점에서는 기울기 값을 정의하기 어려울 수가 있다. 예를 들어 다음 함수는 𝑥=0인 위치에서 기울기를 정의할 수 없다. 이런 경우에는 𝑥=0 에서 미분 불가능(not differentiable)이라고 한다. 반대로 기울기를 구할 수 있으면 미분 가능(differentiable)이라고 한다.
eg. ReLU 함수는 𝑥<0 인 구간에서는 기울기가 0이고 𝑥>0 인 구간에서는 기울기가 1이지만 𝑥=0 인 위치에서는 미분할 수 없다.
기본 미분공식
상수
: 상수를 미분하면 0이 된다.
거듭제곱
: 𝑥의 𝑛 제곱을 미분하면 𝑛−1 제곱으로 제곱수가 1씩 감소한다. 이 공식은 𝑛이 자연수이거나 음의 정수일 때 성립한다. 𝑛=0 일 때는 성립하지 않는다.


로그 ⭐️
: 로그함수를 미분하면 𝑥−1 이 된다.

지수 ⭐️
: 밑이 오일러 수인 지수함수는 미분해도 변하지 않는다.