함수

함수

4.1 함수 — 데이터 사이언스 스쿨

함수는 입력값을 넣으면 출력값을 뱉어냄

정의역(domain): 입력변수가 가질 수 있는 집합(=파라미터)

공역(range): 리턴값(return)

 

변수

: 입력과 출력의 관계를 설명하기 위한 것

-> 입력과 출력의 관계를 학습한 것이 '지도학습 머신러닝'

연속과 불연속

불연속 함수

: 데이터 분석에서 많이 사용됨

부호함수

: 입력이 양수이면 1, 음수이면 -1, 0이면 0을 출력하는 𝑥=0 에서 불연속인 함수

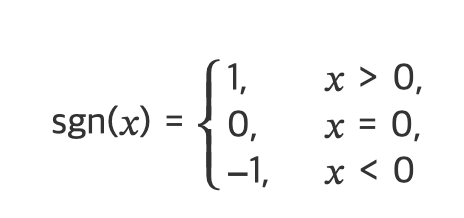
불연속 함수란?
: x가 어떠한 순간에 급격하게 값이 변하는 함수

단위계단함수(Heaviside step function)

: x=0 인 지점에서 불연속인 함수 -> '딥러닝'에서 사용

지시함수(indicator function)

: 함수 이름에 아래 첨자로 미리 지정된 값이 들어오면 출력값이 1이 되고 아니면 0이 출력된다. 

역함수

: 입력/출력 관계와 정반대의 입출력 관계를 갖는 함수이다. 

*함수의 역함수가 존재하려면?

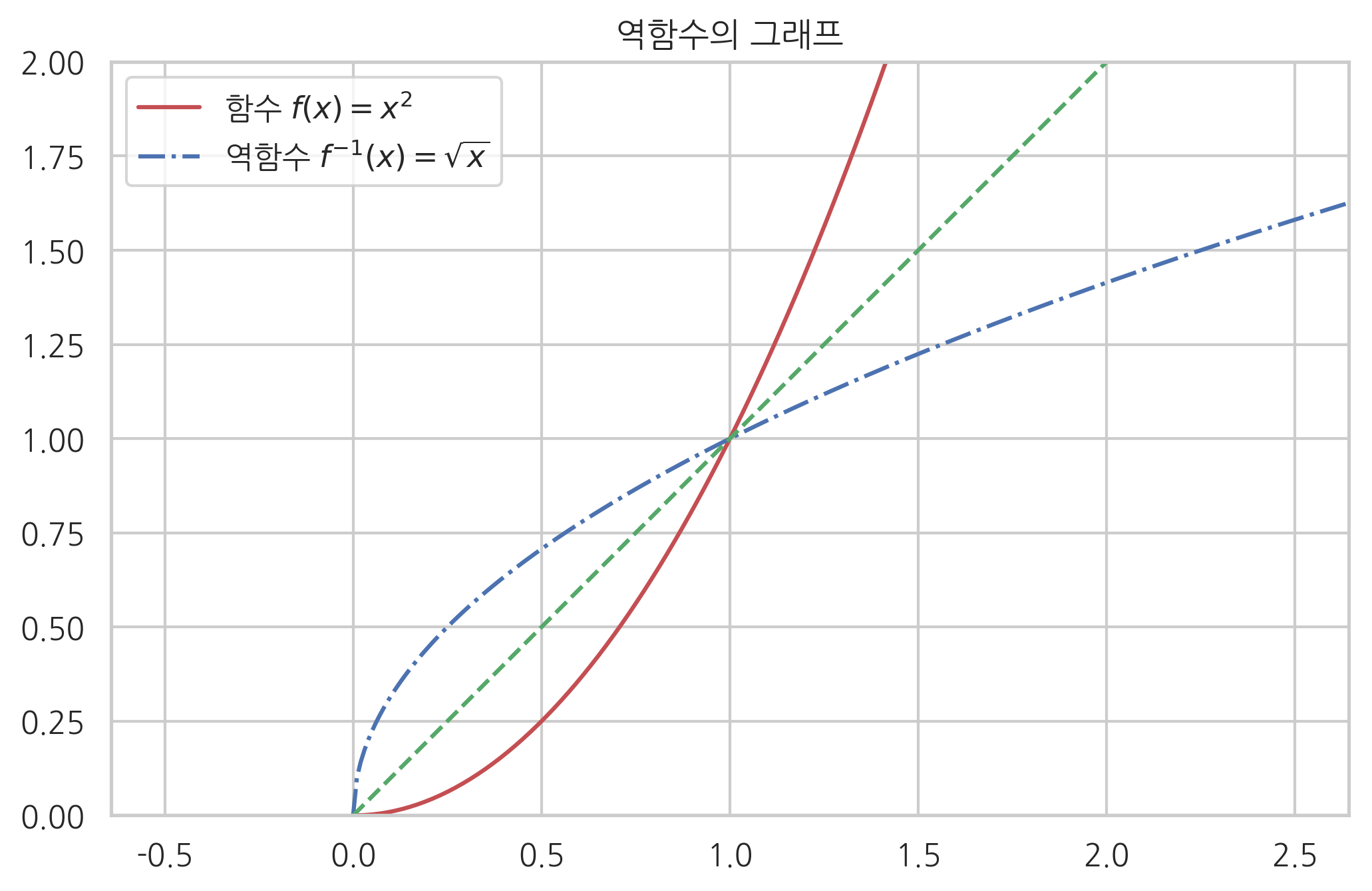
정의역을 양수로 제한해야 한다.(𝑥>0) 이 때는 다음과 같은 역함수가 존재한다.

역함수의 그래프

다항식함수(polynomial function)

*데이터 분석에서 많이 사용됨

하나의 x를 상수항 𝑐0, 일차항 𝑐1𝑥, 이차항 𝑐2𝑥2, ⋯ 등의 거듭제곱 항의 선형조합으로 이루어진 함수

최대함수와 최소함수

• 최대함수: 두 개의 인수 중에서 큰 값을 출력하는 함수
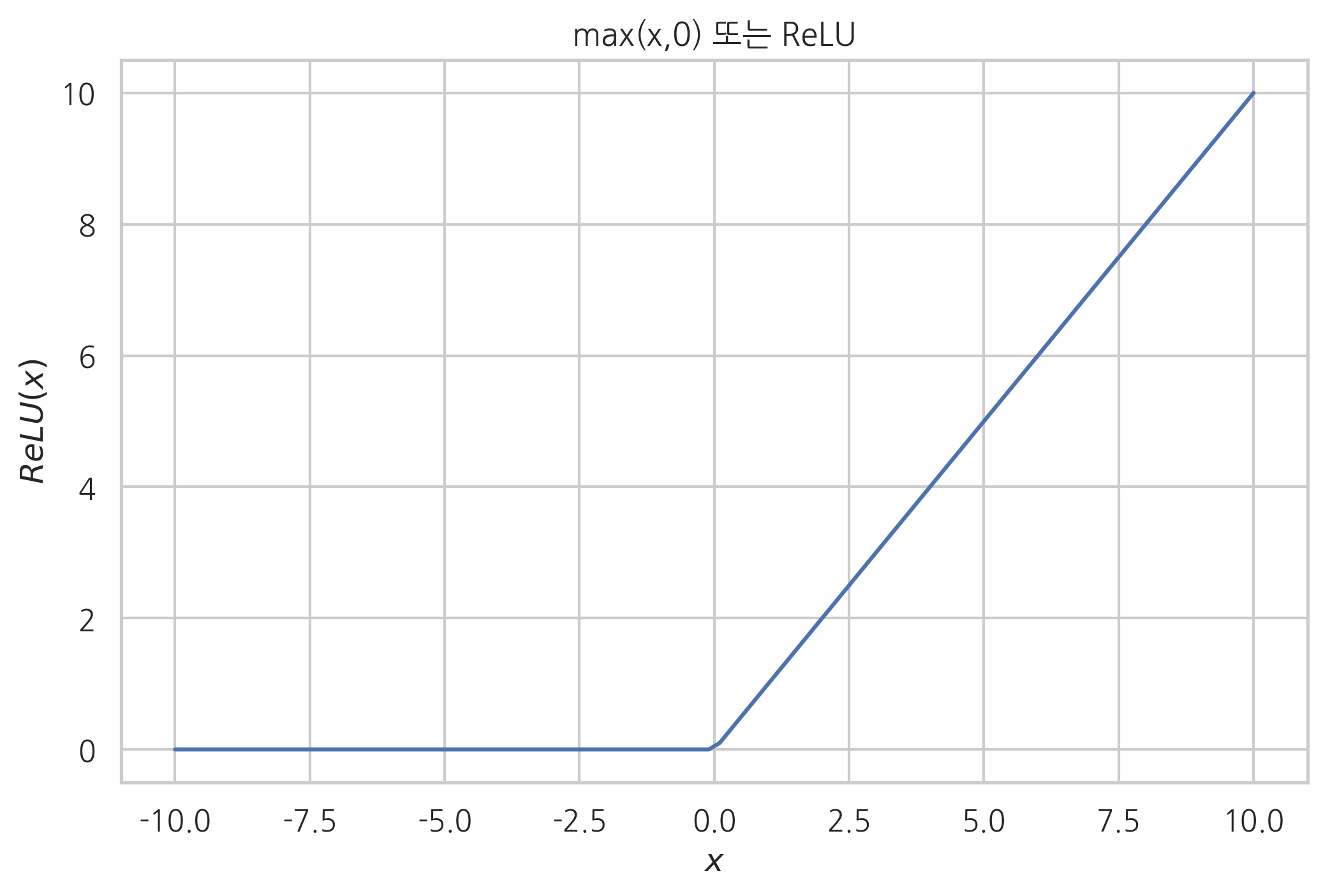
  • 보통 𝑦=0𝑦=0으로 고정해서 입력값 𝑥𝑥가 양수이면 그대로 출력하고 음수일 때는 0으로 만들 때 주로 사용
    • -> 인공신경망에선 이 함수를 ReLU(Rectified Linear Unit)라고 부름
• 최소함수: 최대함수와 반대로 두 개의 인수 중 작은 값을 출력하는 함수

ReLU 함수 ⭐️

(Rectified Linear Unit)

지수함수

 : 거듭제곱을 할 때 아래에 있는 수를 밑(base)라고 하는데 밑을 오일러 수 𝑒(약 2.718)로 하여 거듭제곱을 하는 함수이다.

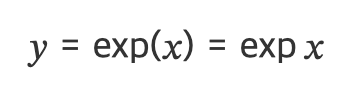
특징

• 양수(𝑒)를 거듭제곱한 값이므로 항상 양수다.
• 𝑥=0일 때 1이 된다.
• 𝑥가 양의 무한대로 가면(𝑥→∞), 양의 무한대로 다가간다.
• 𝑥가 음의 무한대로 가면(𝑥→−∞), 0으로 다가간다.
• 𝑥1>𝑥2이면 exp𝑥1>exp𝑥2이다. (*단조 증가 함수)

로지스틱함수(시그모이드(sigmoid)류 함수)

: 어떠한 데이터를 (입력값 x를) 확률로 해석하기에 용이함(0~1 사이에 위치)

로그함수 

: 지수함수의 역함수, 많이 사용되며 중요함

e를 x제곱해서 y가 된다. 그럼 e를 몇 제곱해야 y가 나올까?

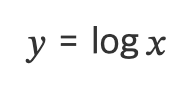
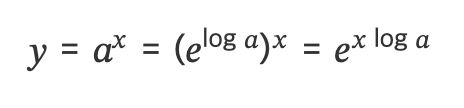
e는 자연상수이므로 ln(자연로그)라고 하기도 함. 

 

특징

• ⭐️ 𝑥값, 즉 입력변수값이 양수이어야 한다. 0이거나 음수이면 정의되지 않는다. 
• 𝑥>1𝑥>1면 𝑦>0𝑦>0 (양수)
• 𝑥=1𝑥=1이면 𝑦=0𝑦=0
• 0<𝑥<10<𝑥<1면 𝑦<0𝑦<0 (음수)
• 𝑥1>𝑥2𝑥1>𝑥2면 log𝑥1>log𝑥2log⁡𝑥1>log⁡𝑥2이다.

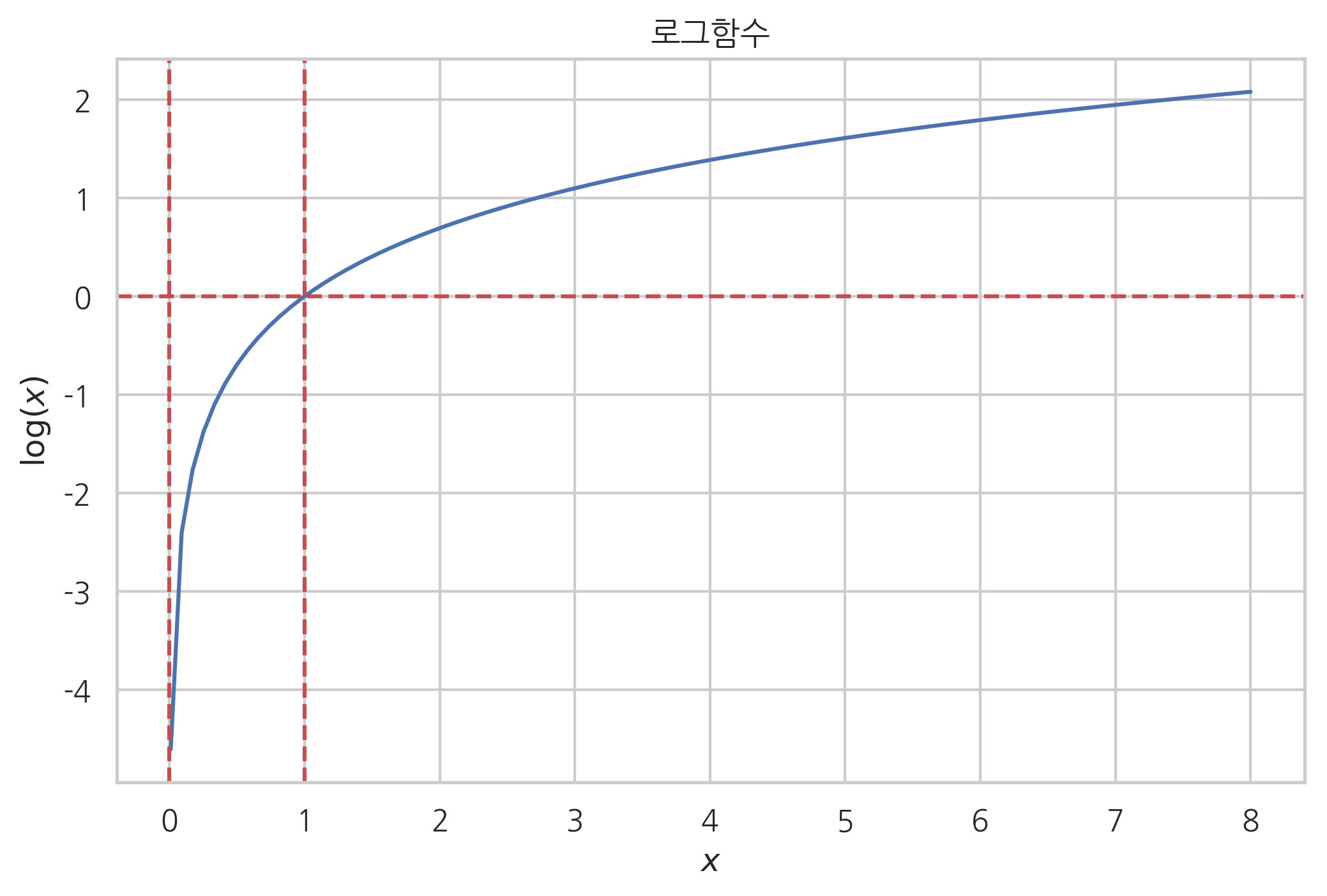
로그함수는 왜 사용할까? ⭐️

1. 로그함수는 곱하기(*)를 더하기(+)로 변환한다.

• log(𝑥1⋅𝑥2)=log𝑥1+log𝑥2

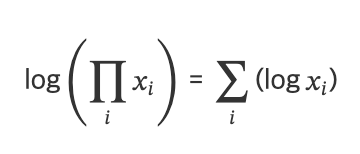
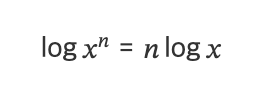
2. 어떤 함수에 로그를 적용해도 함수의 최고점, 최저점의 위치는 변하지 않는다.

: 만약 양수값만을 갖는 함수가 있을 때 이 함수에 다시 로그함수를 적용하면 높낮이는 바뀌지만 최고점이나 최저점의 위치는 바뀌지 않는다. 따라서 최적화할 때 원래의 함수가 아니라 로그를 취한 함수에 대해 최적화를 하는 경우가 많다.

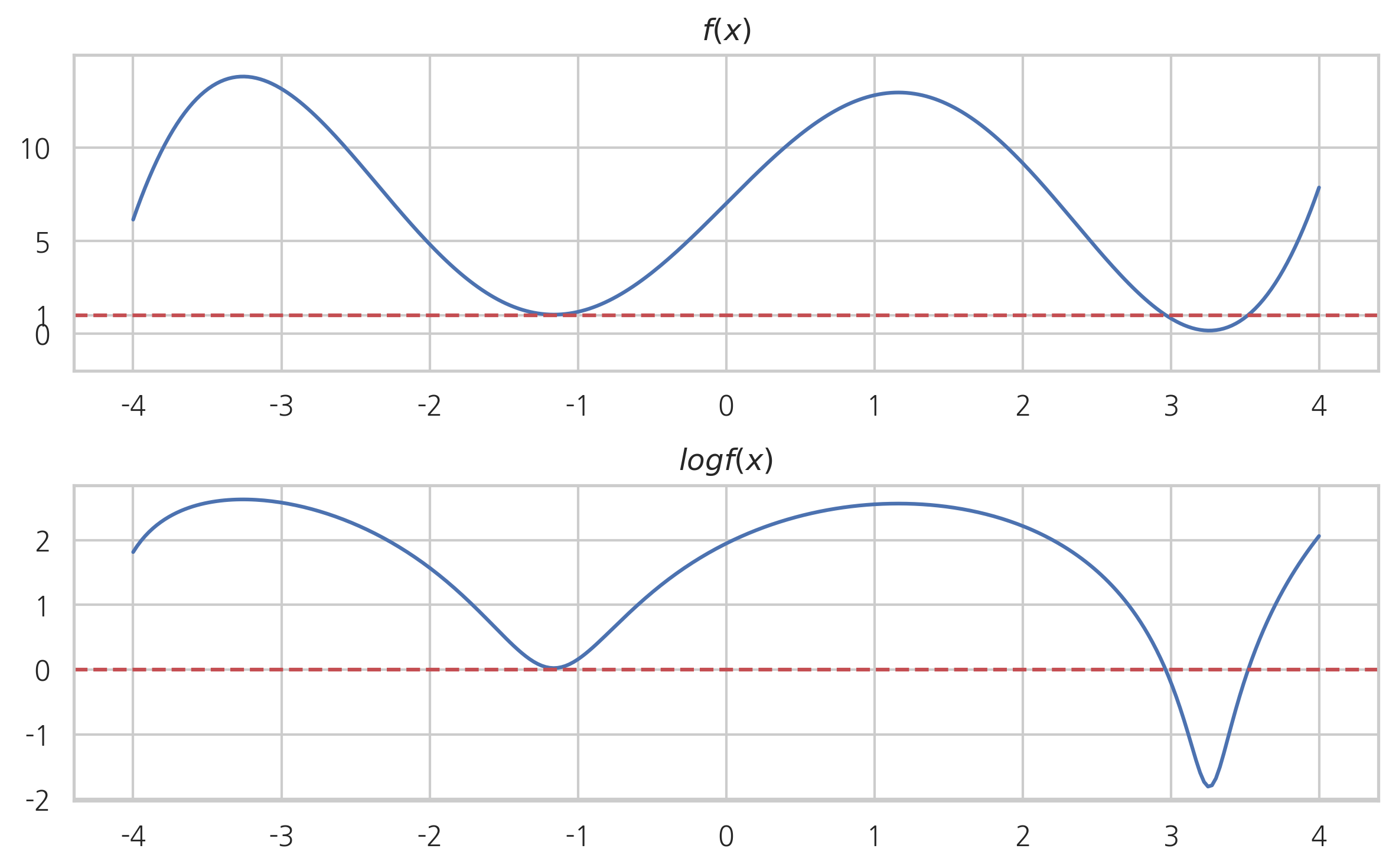
3. 로그함수는 0부터 1사이의 작은 값을 확대시켜 보여준다.

: 로그함수는 0부터 1사이의 구간을 음의 무한대부터 0까지로 확장시켜주기 때문에 확률값처럼 0과 1사이에 있는 작은 값을 더 확실하게 비교할 수 있도록 한다.

---

소프트플러스함수

: 지수함수와 로그함수를 결합하여 만든 함수(*잘 사용하지 않음)

다변수함수

: 변수가 여러개(=복수의 입력변수)

eg. 두 개의 독립변수를 갖는 함수 𝑓(𝑥,𝑦) 의 예로는 위도 𝑥 와 경도 𝑦 를 입력받아 해발 고도 𝑧 를 출력하는 함수

 -> 𝑓(𝑥,𝑦)=2𝑥2+6𝑥𝑦+7𝑦2−26𝑥−54𝑦+107

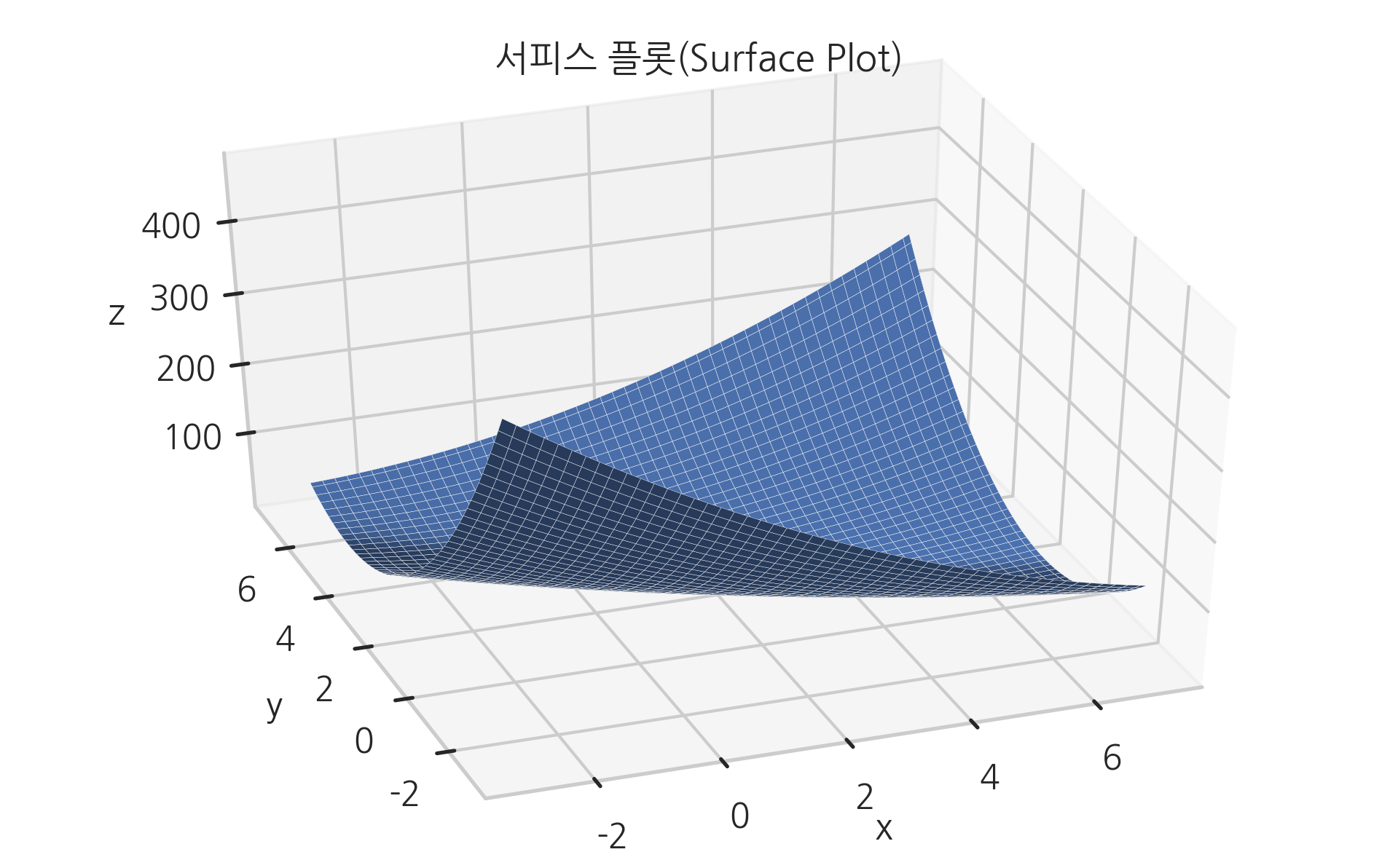
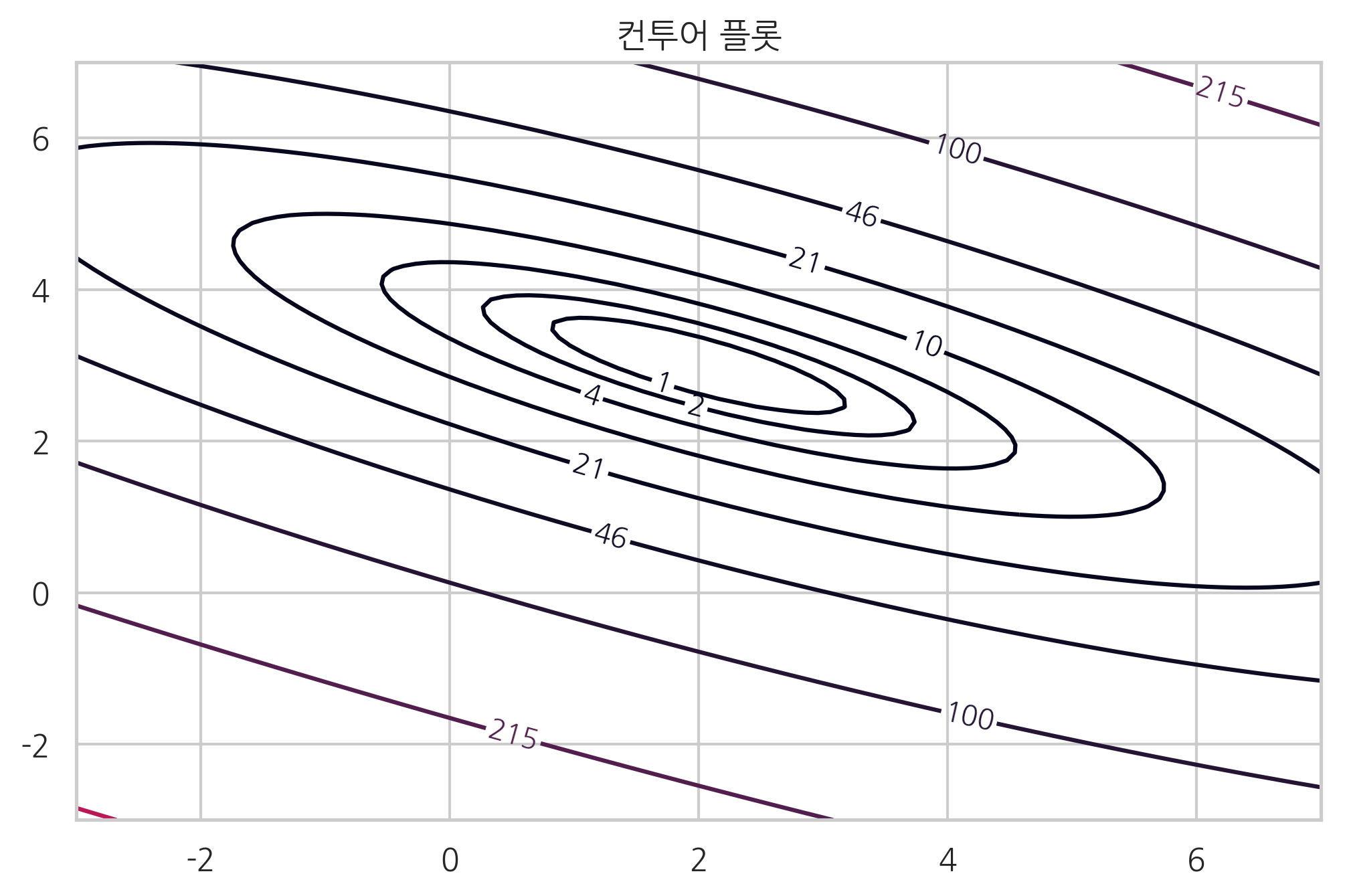
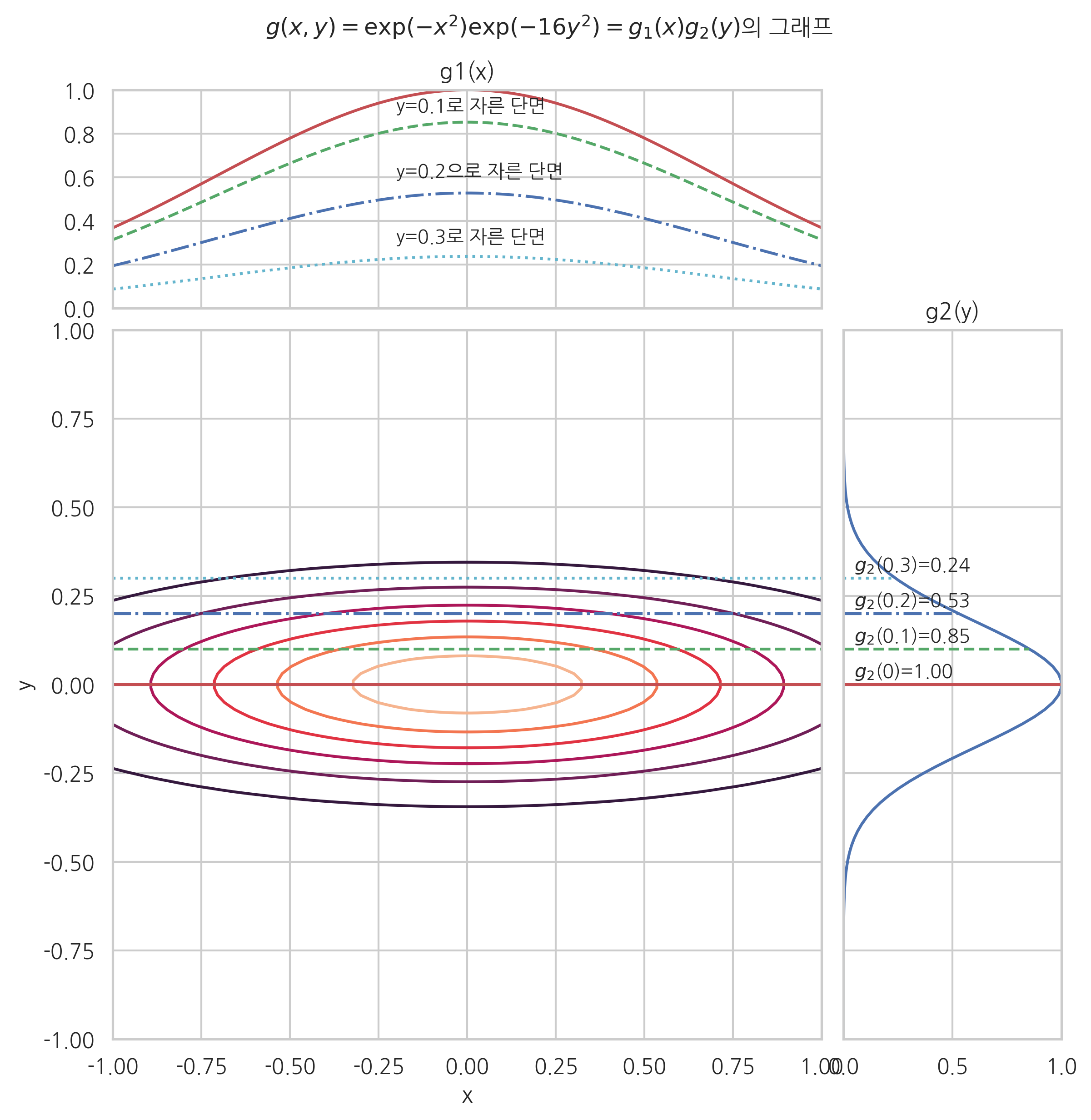
분리 가능 다변수함수

: 2차원 함수는 3차원 공간상의 지형에 비유할 수 있다.